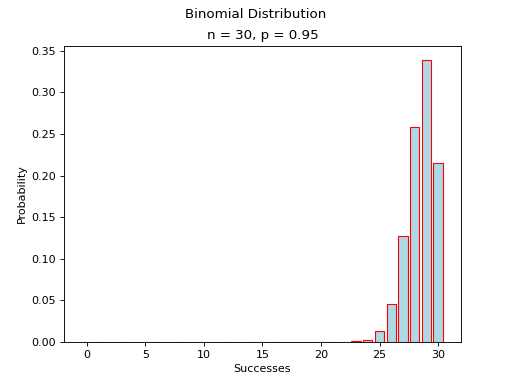
Binomial Distribution#
Motivation#
TODO
Consider a random variable defined as the sum of n Bernoulli random variables,
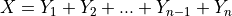
Where each 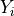 takes the value 1 with probabilitiy p or it takes the value 0 with probabilitiy 1 - p.
takes the value 1 with probabilitiy p or it takes the value 0 with probabilitiy 1 - p.
TODO
From Conditional Probability the probability of an intersection of independent events is the product of individual probabilitiy,
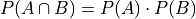
TODO
Probabilitiy Distribution#
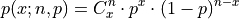
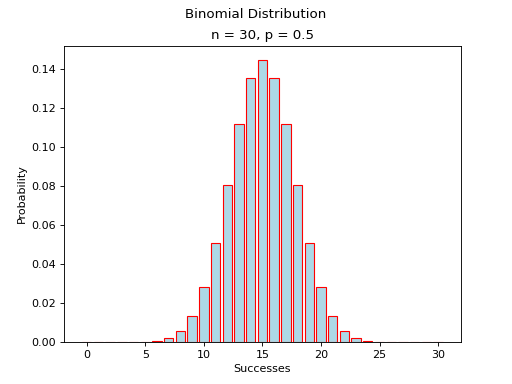
(Source code, png, hires.png, pdf)
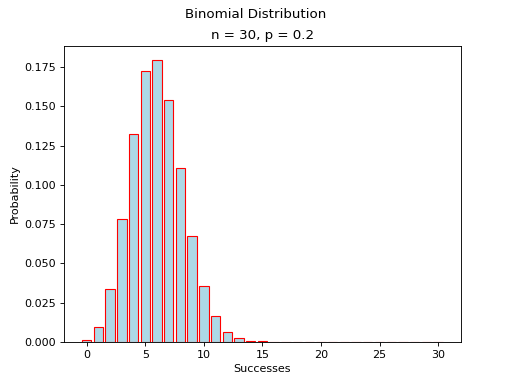
(Source code, png, hires.png, pdf)
(Source code, png, hires.png, pdf)
(Source code, png, hires.png, pdf)