Normal Distribution#
The Normal Distribution is the foundation of inferential statistics.
TODO
Probability Distribution#
(Source code, png, hires.png, pdf)
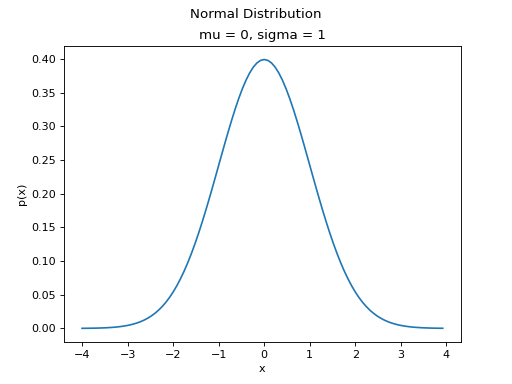
(Source code, png, hires.png, pdf)
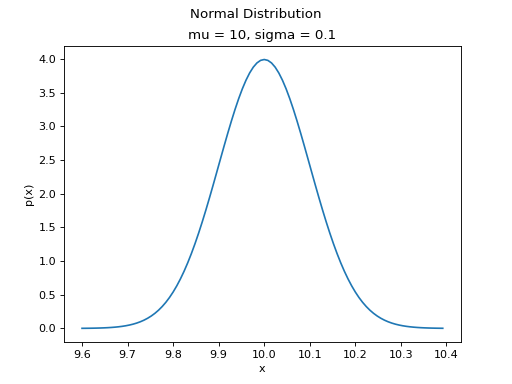
Symmetry#
TODO
Z-Tables#
TODO
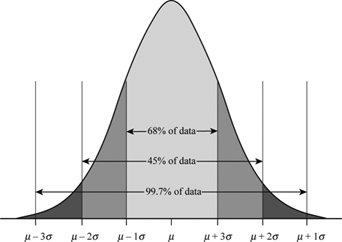
Empirical Rule#
TODO
Pearson Skew Index#
TODO
Effects of Parameters#
Varying the Mean#
TODO
Varying the Standard Deviation#
By changing the Standard Deviation, the shape of the distribution changes. As the Standard Deviation increase, the graph spreads out. This is because Standard Deviation is a measure of variation. In other words, Standard Deviation quantifies how the distribution is spread out along the x-axis.
(Source code, png, hires.png, pdf)
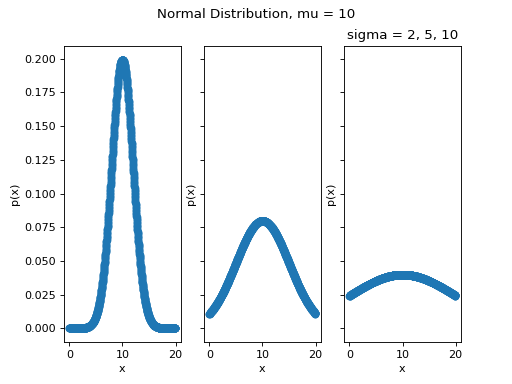
To summarize,
Note
By changing the mean of the normal distribution, the location of the distribution changes.
By changing the standard deviation of the normal distribution, the spread of the distribution changes.
Relation To Other Distributions#
The Normal Distribution is deeply connected with many different areas of mathematics. It pops up everywhere, from quantum mechanics to finance. The reach of the normal distribution is far and wide.
Normal As An Approximation of the Binomial#
TODO
Note
Conditions:
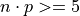
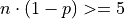
Poisson As An Approximation of the Normal#
TODO
Note
Conditions:
:math:` lambda >> 0`