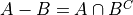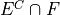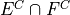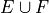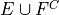Introduction#
Sample Spaces and Events#
Describe the sample spaces of the following experiments with a set using list_notation
Flipping a two-sided coin three times
Rolling a six-sided die
Rolling two six-sided dice
Flipping a two-sided coin and if it lands on heads rolling a six-sided die.
Two dice are rolled. Let E be the event the sum of the outcomes is odd. Let F be the event of at least one 1 appearing on one of the die. Describe the elements of the following evnets in list_notation and interpret the meaning of each event.
Three red balls and one green ball are placed into a box. Describe the samples of the following experiments with a set using List Notation.
Note
Hint: Let r 1, r 2 and r 3 represent the outcome of drawing each of the respective red balls.
Selecting one ball at random.
Selecting two balls at random and with_replacement (i.e. putting the ball you drew back into the back after you draw it).
Selecting two balls at random and without_replacement (i.e. not putting the ball back after you draw it)
A deck of six cards consists of three black cards numbered 1, 2, 3 and three red cards numbered 1, 2, 3. You draw two cards without_replacement. Let A be the event the second card has a larger number than the first card. Let B be the event the first card has a larger number than the second card.
Are A and B mutually exclusive?
Are A and B complements?
Applications#
Let S be the sample space of flipping a fair, two-sided coin three times. LEt A be the event of at least two heads. Find
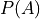
You roll two dice. The find the probability of the following events.
The sum of the numbers rolled is 7.
The sum of the numbers rolled on the dice is 3 or 5.
The numbers rolled are both even.
One of the numbers rolled is even.
Neither or the numbers rolled are even.
Is part e the complement of part c or part d?
You have a standard deck of 52 playing cards. You shuffle the cards into a random order and deal yourself exactly one card. Find the probabilities of the following events,
The card is a king.
The card is a spade.
The card is a king or spade.
The card is a 4 or Jack.
The card is black.
The card is black or a queen.
The card is neither nor a queen.
You select a number randomly between 1 and 1000. What is the probability the number selected is divisible by 5?
Probability Proofs#
Let A and B be two events, not necessarily mutually exclusive. Prove the following inequality
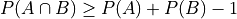
Note
Hint: Use the Law of Unions and Axiom 1
Let A and B be two events, not necessarily mutually exclusive. The event,
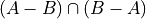
is called the symmetric difference of A and B. Prove the probability of the symmetric difference of A and B is equal to,
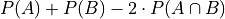
Note
Hint #1: Draw a Venn Diagram of A and B, assuming the events are not mutually exclusive. Label the area that correspodned to the symmetric difference of A and B.
Hint #2: Recall (TODO link)