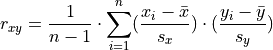Correlation#
Correlation is a measure of the strength of a relationship that exists between two observable variables.
Introduction#
Preliminaries#
Before we can begin our study of correlation, let’s make some preliminary defintions that will help us keep everything clear and precise.
Univariate Statistics#
In order to differentiate between the statistics relationing to the x and y variables, we introduce some notation.
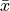 and
and 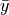 are defined as the univariate sample means of the
are defined as the univariate sample means of the  and
and  variables. In other words,
variables. In other words, 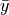 is the sample mean of the
is the sample mean of the  variable, as if we were observing the
variable, as if we were observing the  variable in isolation. Similarly for
variable in isolation. Similarly for 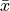 .
.
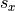 and
and 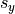 are defined as the univariate standard deviations of the
are defined as the univariate standard deviations of the  and
and  variables. In other words,
variables. In other words, 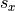 is the standard deviation of the
is the standard deviation of the  variable, as if we were observing the
variable, as if we were observing the  variable in isolation. Similarly, for
variable in isolation. Similarly, for 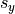 .
.
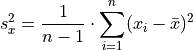
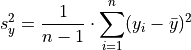
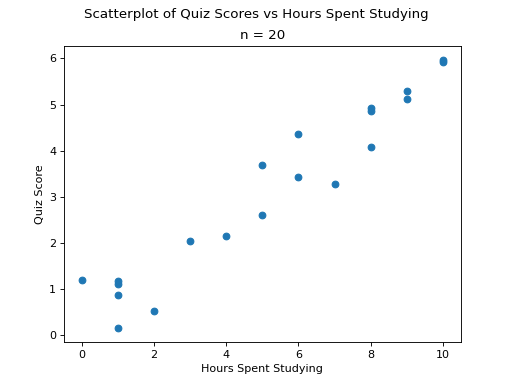
Assessing Correlation#
TODO
(Source code, png, hires.png, pdf)
TODO
(Source code, png, hires.png, pdf)
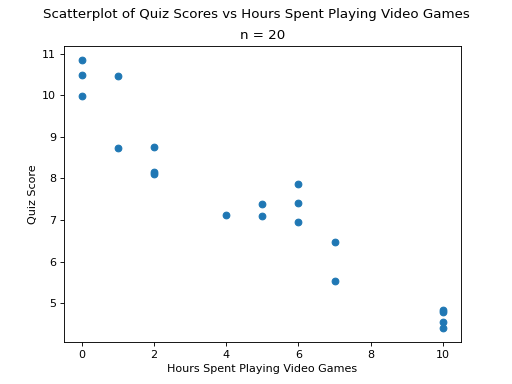
TODO
(Source code, png, hires.png, pdf)
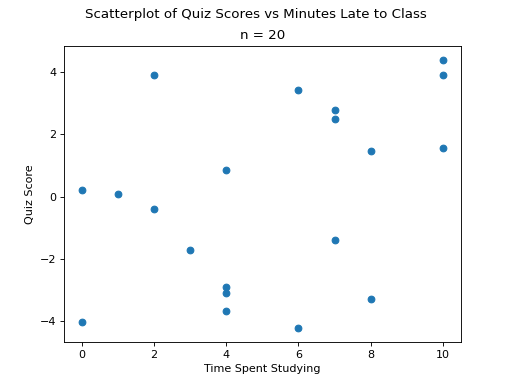
TODO
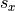 and
and 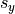 are defined as the univariate standard deviations of the
are defined as the univariate standard deviations of the  and
and  variables. In other words,
variables. In other words, 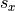 is the standard deviation of the
is the standard deviation of the  variable, as if we were observing only
variable, as if we were observing only  alone. Similarly, for
alone. Similarly, for 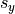 .
.
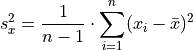
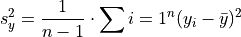
Definition#
Version 1#
TODO: justification. make some plots.
Version 2#
TODO: shortcut for version 2
Version 3#
TODO: justifcation, again.