Geometric Distribution#

TODO

Geometric Random Variable#

Definition#

TODO

Geometric Conditions#

TODO

Parameters#

A Geometric Random Variable has single parameter.

Geometric Distribution#

TODO

Probability Density Function#

TODO

$P(\mathcal{X} = x) = \sum_{i=1}^{x} (1-p)^{x-1} \cdot p$

TODO .. _geometric_cdf:

Cumulative Distribution Function#

TODO

In order to show the geometric density represents a distribution, we must show the probability of all outcomes sums to 1. In order to do this, we must first talk about the geometric series.

Geometric Series#

A geometric series is defined as the sum of powers of r,

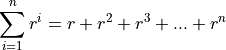
$\sum_{i=1}^{n} r^i = r + r^2 + r^3 + ... + r^n$

The reason it is called geometric can be easily seen if we give r a value. For instance, if 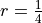$r = \frac{1}{4}$ , then the first few terms of the geometric series are given by,

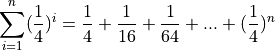
$\sum_{i=1}^{n} (\frac{1}{4})^i = \frac{1}{4} + \frac{1}{16} + \frac{1}{64} + ... + (\frac{1}{4})^n$

Each term on the right hand side can be identified with the areas of successive squares in the following picture,

Geometric Distribution

Contents

Geometric Distribution#

Geometric Random Variable#

Definition#

Geometric Conditions#

Parameters#

Geometric Distribution#

Probability Density Function#

Cumulative Distribution Function#

Geometric Series#

Expectation#