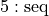Ctrl+K

STATPLOT: Geometric Histogram

STATPLOT: Geometric Histogram#

Introduction#

In a previous section (TODO: link), we introduced the Geometric Distribution. We took a look at the geometPDF function, the probability density function, and the geometCDF, the cumulative distribution function on our TI-83/84 family of calculator. These functions give us quick ways of calculating probabilites for a Geometric Random Variable.

Recall a Geometric Random Variable counts the number of binary trials until a success occurs, where a success occurs in a single trial with probability  and a failure occurs in a single trial with probability. The probability density function for a Geometric Random Variable is given by,

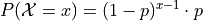
P(\mathcal{X} = x) = (1-p)^{x-1} \cdot p

The domain of this function is defined on all integer values greater than or equal to 1, i.e. 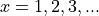x=1,2,3,.... This means the there is non-zero probability for all values of x greater than 1. However, the Geometric PDF still represents the probability distribution of a random variable, and for this reason, the sum of probabilities for 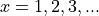x=1,2,3,... cannot exceed 1. Therefore, we expect the probability of x assuming a particular value should go to 0 as the value of x goes to infinity.

Activity#

Let us verify this is the case by plotting a histogram of the Geometric Distribution for the cases where 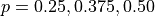p = 0.25, 0.375, 0.50. In order to do this, we will need to generate a list that represents the domain of a Geometric Random Variable. As we just mentioned, the domain of a Geometric Random Variable is infinite, so we will approximate its domain with a suitably large list of values.

Create a sequence of the first 50 natural numbers starting at 1 and store the result in L_1  . .. topic:: Sequence Editor

To insert a sequence into L_1, type in the following commands into a TI-83/84 calculator.

  • \text{BUTTON}: \text{STAT}

  • \text{MENU}: \text{EDIT}

  • \text{1}: \text{EDIT}

This will bring up the List Editor. Use the arrow keys to navigate to the formula bar and press ENTER to start typing a formula,

  • \text{BUTTON}: \text{2ND}

  • \text{BUTTON}: \text{LIST}

  • \text{MENU}: \text{OPS}

  • \text{5}: \text{seq}

(insert picture of sequence editor)

Question #1

Compute the sum of the first 50 natural numbers.

Hint

Use the sum function!

Excellent. This list will represent the (truncated) domain of the Geometric Random Variable. Let’s start with 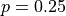p = 0.25. We need to compute the value of the Geometric PDF for every element of the list we just generated.

Go to STAT > EDIT and select the formula bar for  . Go to 2ND > DISTR > E: GEOMETPDF to bring up the Geometric Probability Density Function editor. Pass in the following arguments,



Question #2

  • What is the mean (expected value) of the Geometric Distribution when 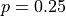p=0.25? Round to three decimal spots.

  • What is the median of the Geometric Distribution when 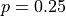p=0.25? Round to three decimal places.

Create a relative frequency histogram using 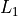L_1 as your XLIST and 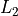L_2 as your FREQ.

Hint

Ensure you have a viewing WINDOW set to,

XMIN: 0

XMAX: 25

XSCL: 1

YMIN: 0

YMAX: 0.5

YSCL: 1

Question #3

Write a few sentences describing the distribution. Be sure to include descriptions of shape, center and variability.

Use the technique just described to generate a new list in 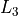L_3 that represents the Geometric Distribution with 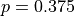p=0.375. Then, generate a second new list in 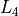L_4 that represents the Geoemtric Distribution with p=0.50.

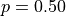Question #4

  • What is the expected value of the Geometric Distribution when 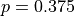p=0.375? Round to three decimal places.

  • What is the expected value of the Geometric Distribution when p=0.5?

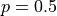Create histograms for all three Geometric Distributions stored in 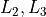L_2, L_3 and L_4.

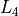Question #5

Compare and contrast the distributions when 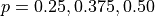p=0.25, 0.375, 0.50. What happens to the Geometric Distribution as the parameter p gets larger? Explain what this means in terms of the Geometric Random Variable.

Solutions#

TODO: jquery these into hidden elements.

  • 1: 1275

  • 2a: 4

  • 2b: 3

  • 4a: 2.667

  • 4b: 2

Contents