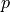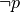Logic#
TODO
Propositions#
- Symbolic Expression
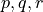
- Definition
A sentence that can be judged either true or false.
TODO
Truth Values#
TODO
Operations#
Negation#
TODO
|
|
T |
F |
F |
T |
Conjunction#
TODO
- Symbolic Expression
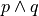
TODO
p |
q |
|
T |
T |
T |
T |
F |
F |
F |
T |
F |
F |
F |
F |
TODO
Disjunction#
TODO
- Symbolic Expression
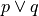
TODO
p |
q |
|
T |
T |
T |
T |
F |
T |
F |
T |
T |
F |
F |
F |
TODO
Implication#
TODO
- Symbolic Expression
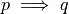
- Definition
A symbolic representation of a conditional (if-then) relationship between two propositions.
This type of proposition can be translated into English in the following ways,
“if p, then q”
“whenever p, then q”
“p implies q”
“q follows from p”
TODO
p |
q |
|
T |
T |
T |
T |
F |
F |
F |
T |
T |
F |
F |
T |
Logical Redundancy#
Logical implication can be expressed in terms of the other logical connectiveS introduced. Notice the range of the implication function assigns a value of True to three of the four value assignments. Logical disjunctions also assigns a value of True to three of the four possible value assignments of its constituent propositions. It is a natural question whether implication can be reduced to disjunction or visa versa.
TODO
Truth Tables#
Compound Propositions#
The logical connectives introduced in the previous section can be used to insert simpler proposition into more complex compound propositions. Compound propositions, while often difficult to understand in plain language, can easily by analyzed in Truth Tables. Examples of Truth Tables were seen in the previous section when logical operations were introduced, but now they will be discussed in more detail.
Value Assignment#
Each row of a Truth Table represents a different value assignment to the constituent propositions involved in the compound proposition. For example, in the case of “p or q”, the compound symbolic proposition is 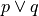. A truth table is constructed by listing every possible combination of truth value for p and q,
p |
q |
|
T |
T |
T |
T |
F |
T |
F |
T |
T |
F |
F |
F |
The first two columns represent the input propositions and their respective truth-values. The third column represents the output proposition and the truth-value that results from that particular value assignment.
Each row details a different state of the world. The list is exhaustive because every possible combination is contained in the table. Therefore, by looking at the table, we know in which cases we can correctly say .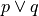
Tautologies#
TODO
Contradictions#
TODO
Carnap’s Method#
TODO
Quantification#
TODO
Universal Quantification#
- Symbolic Expression
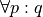
- Definition
A symbolic representation of a universal proposition.
This type of proposition can be translated into English in the following ways,
“for all p, q”
“for every p, q”
“for each p, q”
TODO
Existential Quantification#
- Symbolic Expression
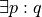
- Definition
A symbolic representation of an existential proposition.
This type of proposition can be translated into English in the following ways,
“there exists a p such that q”
“for some p, q”
“there is a p that q”
Logical Inference#
Law of Detachment#
The Law of Detachment is a symbolic representation of deductive logic. The truth of an implication is asserted in conjunction with the truth of its hypothesis, which leads to the truth of the implication’s consequence. Symbolically,
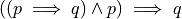
TODO
Note
The Law of Detachment is often known by its Latin name, modus ponens.
TODO
Symbolic Arguments#
The hypothesis in the Law of Detachment