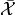Confidence Intervals#

Definitions#

Critical Value#

Standard Error#

Margin of Error#

Intervals#

Problems#

Introduction#

Critical Values

The time it takes a given AP Statistics student to finish one of Mr. Moore’s exams is Normally distributed with a mean of 50 minutes and a standard deviation of 10 minutes. You draw a simple random sample of 30 AP Statistics students and force them to take one of Mr. Moore’s exams. You record the time it takes each individual in your sample to complete the exam and calculate the average.

Describe the sampling distribution for the average amount of time it takes a sample of this many AP statistics students to complete Mr. Moore’s exam. What are the mean and standard deviation of the sampling distribution?

Find the standardized critical values for the following confidence levels:

90%

95%

99%

Using the Z-score formula $z = \frac{ \bar{x} - \mu }{ \frac{s}{\sqrt{n}} }$ , find the values of the sample mean that correspond to the following confidence levels:

90%

95%

99%

Draw three Normal curves for the sampling distribution of the sample mean of exam times. For each confidence level in part b, label the critical values on the horizontal axis of one of the graphs. Shade in the area that corresponds to the given confidence level on that graph.

Using the graphs from part d, write a few sentences interpretting the calculated values from part c.

Using the graphs from part d, what conclusion can you draw about the relationship between the width of the estimation interval (i.e., the precision of the estimate) and the confidence level.

Error

According to the most recent estimates (by which I mean, whatever the top result on Google said), approximately 8% of males are born colorblind.

Find the standard error for the proportion of males that are color blind in a sample of 100 males.

Find the standard error for the proportion of males that are color blind in a sample of 150 males.

Find the standard error for the proportion of males that are color blind in a sample of 200 males.

What is the relationship between the standard error and the number of samples? What does this tell you about the shape of the sampling distribution as n increases?

How large of a sample would you need to get a margin of error that is no more than 0.04?

How large of a sample would you need to get a margin of error that is no more than 0.01?

How large of a sample would you need to get a margin of error that is no more than 0.001?

What is the relationship between the width of the margin of error and the number of samples? How many samples would you need to get a margin of error equal to 0?

Estimates

After careful measurement over the school year, Mr. Moore is 95% confident the average amount of time Sejal spends studying over the week is between 0.10 hours and 0.55 hours.

What is the margin of error on Mr. Moore’s estimate for Sejal’s study time?

What is Mr. Moore’s point estimate for the average amount of time Sejal spends studying a week?

What is the standard error associated with Mr. Moore’s estimation interval?

Modern Mathematical Statistics, Devore & Berk, 2007, Chapter 8.1 #2

Each of the following is a confidence interval for 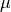$\mu$ , the true average (i.e., population mean) resonance frequency (Hz) for all tennis rackets of a certain type

(114.4, 115.6)

(144.1, 115.9)

Use this information to answer the following questions.

What is the value of the sample mean resonance frequency?

Both intervals were calculated from the same sample data. The confidence level for one of these intervals is 90% and for the other is 99%. Which of the intervals has the 90% confidence level, and why?

Modern Mathematical Statistics, Devore & Berk, 2007, Chapter 8.1 #3

Suppose that a random sample of 50 bottles of a particular brand of cough syrup is selected and the alcohol content of each bottle is determined. Let 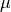$\mu$ denote the average alcohol content for the population of all bottles of the brand under study. Suppose that the resulting 95% confidence interval is :math`(7.8, 94)`.

Would a 90% confidence interval calculated from this same sample have been narrower or wider than the given interval? Explain your reasoning.

Consider the following statement: There is a 95% chance that $\mu$ is between 7.8 and 9.4. Is this statement correct? Why or why not?

Consider the following statement: We can be highly confident that 95% of all bottles of this type of cough syrup have an alcohol content that is between 7.8 and 9.4. Is this statement correct? Why or why not?

Consider the following statement: If the process of selecting a sample of size 50 and then computing the corresponding 95% interval is repeated 100 times, approximately 95 of the resulting intervals will include $\mu$ . Is this statement correct? Why or why not?

Population Proportion#

OpenStax, Statistics, Chapter 8: #118

Suppose that insurance companies did conduct a survey. They randomly surveyed 400 drivers and found that 320 claimed they always buckle up. We are interested in the population proportion of drivers who claim they always buckle up.

Define the random variables $\mathcal{X}$ and $\hat{p}$ in words.

Which distribution should you use for this problem? Explain your choice.

Construct a 95 percent confidence interval for the population proportion who claim they always buckle up.

Find the standard error.

Find the margin of error.

State the confidence interval

Sketch the graph. Label the interval limits and confidence level on the graph.

Difference of Proportions#

Introductory Statistics, Shafer & Zhang, Chapter 7.3: 18

A survey of 21,250 households concerning telephone service gave the results shown in the following table,

	Landline	No Landline
Cellphone	12,474	5,844
No Cellphone	2,529	403

Use this information to answer the following questions.

Give a point estimate for the proportion of households with landlines that also own a cellphone.

Give a point estimate for the proportion of households without landlines that also own a cellphone.

Verify the conditions for inference have been met for the sampling distribution of the difference of sample proportions.

Find the standard error for the sampling distribution.

Construct a 95% confidence interval for the difference in the proportion of households with landlines that use cellphones and the proportion of households without landlines that use cellphones.

Write a few sentences interpretting the results in part e.

Based on the answers to part e and part f, is there evidence to support the conclusion households without landlines are more likely to own cellphones than households with landlines? Justify your answer.

Population Mean#

Modern Mathematical Statistics, Devore & Berk, 2007, Chapter 8.1 #6

On the basis of extensive tests, the yield point of a particular type of mild steel reinforcing bar is known to be normally distributed with 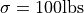$\sigma = 100 \text{lbs}$ . The composition of the bar has been slightly modified, but the modification is not believed to have affected either the normality of the value of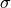 $\sigma$

Assuming this to be the case, if a sample of 25 modified bars resulted in a sample average yield of 8439 lbs, compute a 90% Confidence Interval for the true average yield point of the modified bar.

How would you modify the interval in part a to obtain a confidence of 92%?

OpenStax, Statistics, Chapter 8: #2

Suppose that an accounting firm does a study to determine the time needed to complete one person’s tax forms. It randomly surveys 100 people. The sample mean is 23.6 hours. There is a known population standard deviation of 7.0 hours. Moreover, the population distribution is assumed to be normal.

Define the random variables $\mathcal{X}$ and $\mathcal{\bar{X}}$

Which distribution should you use for this problem? Explain your choice.

Construct a 90 percent confidence interval for the population mean time to complete the tax forms.

Find the standard error.

Calculate the margin of error.

State the confidence interval.

Sketch the graph. Label the interval limits and confidence level on the graph.

If the firm wished to increase its level of confidence and keep the error bound the same by taking another survey, which changes should it make?

If the firm did another survey, kept the error bound the same, and only surveyed 49 people, what would happen to the level of confidence? Why?

Suppose that the firm decided that it needed to be at least 96 percent confident of the population mean length of time to within one hour. How would the number of people the firm surveys change? Why?

Difference of Means#

Heights

The heights of males in the United States have a distribution with a standard deviation of 3 inches. The heights of females in the United States have a distribution with a standard deviation of 2 inches.

Suppose you randomly sample 30 females and 35 males from the United States. You calculate the sample mean for the females to be 64.3 inches and the sample mean for the males to be 67.5 inches.

Describe the sampling distribution for the sample mean of male heights, i.e. what are its expected value and variance?

Describe the sampling distribution for the sample mean of female heights, i.e. what are its expected value and variance?

What is the point estimate for the difference between the average male height and the average female height?

What is the standard error associated with the point estimate in part c?

Assuming there is no difference between the average male height and the average female height, describe the sampling distribution for the difference of average male height and average female height.

Construct a 95% confidence interval for the difference between the true mean of male heights and the true mean of female heights.

Based on the answer to part g, do you have evidence to conclude the average height of males is greater than the average height of females? Justify your answer.

A.P. Exam Practice#

Means#

2004, Free Response Form B, #4

The principal at Crest Middle School, which enrolls only sixth-grade students and seventh-grade students, is interested in determining how much time students at that school spend on homework each night. The table below shows the mean and standard deviation of the amount of time spent on homework each night (in minutes) for a random sample of 20 sixth-grade students and a separate random sample of 20 seventh-grade students at this school.

	Mean	Standard Deviation
Sixth-grade students	27.3	10.8
Seventh-grade students	47.0	12.4

Based on dotplots of these data, it is not unreasonable to assume that the distribution of times for each grade were approximately normally distributed.

Estimate the difference in mean times spent on homework for all sixth- and seventh-grade students in this school using an interval. Be sure to interpret your interval.

An assistant principal reasoned that a much narrower confidence interval could be obtained if the students were paired based on their responses; for example, pairing the sixth-grade student and the seventh-grade student with the highest number of minutes spent on homework, the sixth-grade student and seventh-grade student with the next highest number of minutes spent on homework, and so on. Is the assistant principal correct in thinking that matching students in this way and then computing a matched-pairs confidence interval for the mean difference in time spent on homework is a better procedure than the one used in part a ? Explain why or why not.

2009, Free Response, #4

One of the two fire stations in a certain town responds to calls in the northern half of the town, and the other fire station responds to calls in the southern half of the town. One of the town council members believes that the two fire stations have different mean response times. Response time is measured by the difference between the time an emergency call comes into the fire station and the time the first fire truck arrives at the scene of the fire.

Data were collected to investigate whether the council member’s belief is correct. A random sample of 50 calls selected from the northern fire station had a mean response time of 4.3 minutes with a standard deviation of 3.7 minutes. A random sample of 50 calls selected from the southern fire station had a mean response time of 5.3 minutes with a standard deviation of 3.2 minutes.

Construct and interpret a 95 percent confidence interval for the difference in mean response times between the two fire stations.

Does the confidence interval in part (a) support the council member’s belief that the two fire stations have different mean response times? Explain.

2006, Free Response, #4

Patients with heart-attack symptoms arrive at an emergency room either by ambulance or self-transportation provided by themselves, family, or friends. When a patient arrives at the emergency room, the time of arrival is recorded. The time when the patient’s diagnostic treatment begins is also recorded.

An administrator of a large hospital wanted to determine whether the mean wait time (time between arrival and diagnostic treatment) for patients with heart-attack symptoms differs according to the mode of transportation. A random sample of 150 patients with heart-attack symptoms who had reported to the emergency room was selected. For each patient, the mode of transportation and wait time were recorded. Summary statistics for each mode of transportation are shown in the table below.

Mode of Transportation	Sample Size	Mean Wait Time (minutes)	Standard Deviation of Wait Time (minutes)
Ambulance	77	6.04	4.30
Self	73	8.30	5.16

Use this information to solve the following problems.

Use a 99 percent confidence interval to estimate the difference between the mean wait times for ambulance-

transported patients and self-transported patients at this emergency room.

Based only on this confidence interval, do you think the difference in the mean wait times is statistically

significant? Justify your answer.

Proportions#

2010, Free Response Form B, #4

A husband and wife, Mike and Lori, share a digital music player that has a feature that randomly selects which song to play. A total of 2,384 songs were loaded onto the player, some by Mike and the rest by Lori. Suppose that when the player was in the random-selection mode, 13 of the first 50 songs selected were songs loaded by Lori.

Construct and interpret a 90 percent confidence interval for the proportion of songs on the player that were loaded by Lori.

Mike and Lori are unsure about whether the player samples the songs with replacement or without replacement when the player is in random-selection mode. Explain why this distinction is not important for the construction of the interval in part a.

2010, Free Response, #3

A humane society wanted to estimate with 95 percent confidence the proportion of households in its county that own at least one dog. The humane society selected a random sample of households in its county and used the sample to estimate the proportion of all households that own at least one dog. The conditions for calculating a 95 percent confidence interval for the proportion of households in this county that own at least one dog were checked and verified, and the resulting confidence interval was 0.417 ± 0.119.

Interpret the 95 percent confidence level in this context.

A national pet products association claimed that 39 percent of all American households owned at least one dog. Does the humane society’s interval estimate provide evidence that the proportion of dog owners in its county is different from the claimed national proportion? Explain.

How many households were selected in the humane society’s sample? Show how you obtained your answer.

2022, Free Response, #4

A survey conducted by a national research center asked a random sample of 920 teenagers in the United States how often they use a video streaming service. From the sample, 59% answered that they use a video streaming service every day.

Construct and interpret a 95% confidence interval for the proportion of all teenagers in the United States who would respond that they use a video streaming service every day.

Based on the confidence interval in part a, do the sample data provide convincing statistical evidence that the proportion of all teenagers in the United States who would respond that they use a video streaming service every day is not 0.5 ? Justify your answer.

2018, Free Response, #2

An environmental science teacher at a high school with a large population of students wanted to estimate the proportion of students at the school who regularly recycle plastic bottles. The teacher selected a random sample of students at the school to survey. Each selected student went into the teacher’s office, one at a time, and was asked to respond yes or no to the following question.

Do you regularly recycle plastic bottles?

Based on the responses, a 95 percent confidence interval for the proportion of all students at the school who would respond yes to the question was calculated as 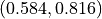$(0.584, 0.816)$ .

How many students were in the sample selected by the environmental science teacher?

Given the method used by the environmental science teacher to collect the responses, explain how bias might have been introduced and describe how the bias might affect the point estimate of the proportion of all students at the school who would respond yes to the question.

The statistics teacher at the high school was concerned about the potential bias in the survey. To obtain a potentially less biased estimate of the proportion, the statistics teacher used an alternate method for collecting student responses. A random sample of 300 students was selected, and each student was given the following instructions on how to respond to the question.

In private, flip a fair coin.

If heads, you must respond no, regardless of whether you regularly recycle.

If tails, please truthfully respond yes or no.

What is the expected number of students from the sample of 300 who would be required to respond no because the coin flip resulted in heads?

The results of the sample showed that 213 of the 300 selected students responded no. Based on the results of the sample, give a point estimate for the proportion of all students at the high school who would respond yes to the question.

2017, Free Response, #2

The manager of a local fast-food restaurant is concerned about customers who ask for a water cup when placing an order but fill the cup with a soft drink from the beverage fountain instead of filling the cup with water. The manager selected a random sample of 80 customers who asked for a water cup when placing an order and found that 23 of those customers filled the cup with a soft drink from the beverage fountain.

Construct and interpret a 95 percent confidence interval for the proportion of all customers who, having asked for a water cup when placing an order, will fill the cup with a soft drink from the beverage fountain.

The manager estimates that each customer who asks for a water cup but fills it with a soft drink costs the restaurant $0.25. Suppose that in the month of June 3,000 customers ask for a water cup when placing an order. Use the confidence interval constructed in part (a) to give an interval estimate for the cost to the restaurant for the month of June from the customers who ask for a water cup but fill the cup with a soft drink.