Try this in your .rst file:

const problems = [ { id: "ti_geometpdf_01a", answers: [ 0.018 ] } ]; function handleInput(event) { console.log(event); if(event.key == "Enter") { event.preventDefault(); var corretAnswers = problems.filter( problem => problem.id === event.target.id).pop().answers var userAnswer = document.getElementById(event.target.id).value if (corretAnswers.includes(userAnswer)) { console.log("happy fun time"); } else { console.log("awful bad time") } } } problems.forEach( problem => { var input = document.getElementById(problem.id); if(input) input.addEventListener("keypress", handleInput) });

GEOMETPDF: Geometric Probabilities

Introduction

The Geometric Distribution is defined as the probability distribution for a Geometric Random Variable. A Geometric Random Variable coutns the number of trials until the first success.

Suppose 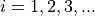random trials are performed, where each trial is either a success with probability p or a failure with probability 1-p; Furthermore, each trial has the same probability of success and the same probability of failure. If these conditions are met, a Geometric Random Variable counts the number of trials until the first instance of success.

The following card summarize the conditions that must be met to model a random process with a Geometric Random Variable,

Condition for Geometric Random Variable

1. A sequence of independent trials are performed.

2. There are only two possible outcomes for each trials, success or failure.

3. The probability of success, p, is the same for every trial.

For example, suppose we flip a coin until we get a head. Further suppose we are interested in the probability of flipping the coin three times before we get a head, i.e. the first head occurs on the third flip. Symbolically,

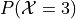
If the third trial is a success, then the first two were failures. By the independence of each trial and Bayes’ multiplication laws, the probability can be calculated,

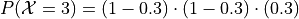
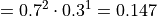
In general,

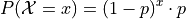
The probability of success, p, is the single parameter of the Geometric Distribution. The quantity P(mathcal{X}=x) is called the probability density function, sometimes shortened to simply PDF.

Calculator

Geometric Probability Density Function

The following sequence will bring up the geometPDF function on the TI-83/84 family of calculators,

• 

• 

• 

• 

The geometPDF menu requires two arguments,

1. p: a probability of success for a single trial.

2. x: the number of trials whose probability is sought.

(TODO: insert picture of GEOMETPDF menu)

Problems

1. A manufacturer produces a large quantity of computer components each day. Assume that the probability of a defective computer component being produced is 0.02. Components are randomly selected from a manufacturer’s assembly line.

   1. Find the probability that the first defect is caused by the seventh component tested. Round to three decimal places.

   2. What is the probability the first defect is caused by the sixth or seventh component tested? Round to three decimal places.

   3. What is the probability of having to test at least three components before you find a defective one? Round to three decimal places.

2. Suppose you flip a coin until you get heads. What is the probability you will flip the coin exactly five times? Round to three decimal places.

3. Suppose you roll a six-sided die until you get a face that shows a 4. What is the probability you will roll the die exactly three times? Round to three decimal places.

4. Suppose you roll two six-sided dice until the sum of the outcomes on both faces is greater than 9. What is the probability you will need to roll the dice at least three times? Round to three decimal places.

Solutions

TODO: jquery these with a submit button.

1a: 0.018 1b: 0.036 1c: 0.960 2: 0.031 3: 0.116 4: 0.694