Bernoulli Distribution#
TODO
Bernoulli Random Variable#
A Bernoulli random variable 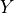 is defined for experiments where the only outcomes are “success” and “failure”, which we denote
is defined for experiments where the only outcomes are “success” and “failure”, which we denote  and
and  , respectively. The sample_space for a Bernoulli random variable is given by,
, respectively. The sample_space for a Bernoulli random variable is given by,
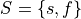
A Bernoulli random variable 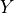 takes on the value of
takes on the value of 1 when a success occurs and it takes on the value of 0 when a failure occurs. In other words,
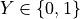
Probability Density#
TODO
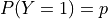
By the Law of Complements, the probability of a 0 is,
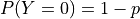
We can summarize these results as follows,
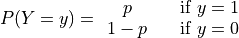
Distribution#
TODO