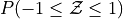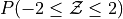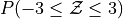Ctrl+K

Normal Distribution

Normal Distribution#

Introduction#

Standard Normal#

  1. Sketch a Standard Normal distribution in the x-y plane. Shade in the areas indicated in the problems below. Label the axes. Label each area with the percentage of the distribution that corresponds to the shaded region. Use a Z Table to find the exact percentage.

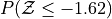
    1. P(\mathcal{Z} \leq -1.62)

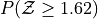
    2. P(\mathcal{Z} \geq 1.62)

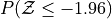
    3. P(\mathcal{Z} \leq -1.96)

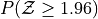
    4. P(\mathcal{Z} \geq 1.96)

    5. What is the relationship between parts a and b, and parts c and d? What characteristic of the Standard Normal distribution is being shown here?

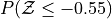
    6. P(\mathcal{Z} \leq -0.55)

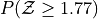
    7. P(\mathcal{Z} \geq 1.77)

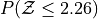
    8. P(\mathcal{Z} \leq 2.26)

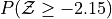
    9. P(\mathcal{Z} \geq -2.15)

  2. Sketch a Standard Normal distribution in the x-y plane. Shade in the areas indicated in the problems below. Label the axes. Label each area with the percentage of the distribution that corresponds to the shaded region. Use a Z Table to find the exact percentage.

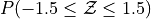
    1. P(-1.5 \leq \mathcal{Z} \leq 1.5)

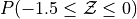
    2. P(-1.5 \leq \mathcal{Z} \leq 0)

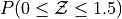
    3. P(0 \leq \mathcal{Z} \leq 1.5)

    4. What is the relationship between parts a, b and c? Explain the result graphically.

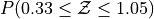
    5. P(0.33 \leq \mathcal{Z} \leq 1.05)

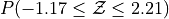
    6. P(-1.17 \leq \mathcal{Z} \leq 2.21)

  3. Sketch a Standard Normal distribution in the x-y plane. Find the values of Z which correspond to the areas given below. Shade in the areas and label the axes with the value found. Use a Z Table to solve the problem.

    1. 0.90

    2. 0.75

    3. 0.5

    4. 0.25

    5. 0.10

  4. The Empirical Rule

Since the Z-Table is the cumulative distribution function for the Standard Normal distribution, The Empirical Rule can be derived through a Z-table. Recall the Empirical Rule states,

This can be stated more precisely in terms of the Z distributions as follows,

The Empirical Rule is an approximation, meant for quick calculations. It is not exact, as you will soon discover.

  1. Use a Z Table to find the exact value of P(-1 \leq \mathcal{Z} \leq 1)

  2. Use a Z Table to find the exact value of P(-2 \leq \mathcal{Z} \leq 2)

  3. Use a Z Table to find the exact value of P(-3 \leq \mathcal{Z} \leq 3)

Non-standard Normal#

TODO

A.P. Exam Practice#

TODO: need to find normal only (i.e. no central limit theorem or random variable linear combinations)

Contents