Probability Bingo

Probability Bingo is a fun way to think about randomness!

Required Materials

• Various kinds of dice (3-sided, 6-sided, 12-sided, 24-sided, 30-sided, 50-sided, etc.)

• Paper

• Pencil

• Optional: Prize for winner

Rules

Each player should construct a 5 by 5 bingo square on a sheet of paper,

(TODO: INSERT PICTURE)

Once all the game cards have been created, the host will reveal a pair of dice being used for the round. The players will then be given the opportunity to fill in their bingo squares. The players may fill in the squares with any numbers they wish.

The host will then roll the dice he or she has selected. The sum of the faces on both die will be counted as the bingo call for that draw. The players will check their game cards for matches. If any of their numbers match the called number, they will cross out one square per turn.

For example, if the host rolls a 4 and a 3, the bingo call will be 4 + 3 = 7. Any player with a 7 on their card will cross out that 7. If a player has more than one 7 on their card, they can only cross out one. In other words, players may only cross out a single number each time a number is called.

When a player forms a row, column or diagonal with crossed out numbers, he or she will yell “Bingo!” and be crowned the winner.

Problems

1. Draw the sample space for each round of probability bingo. How is the sample space affected by the number of faces on the die chosen by the host?

2. An optimal strategy is a player strategy that is most likely to win.

   1. If the host chooses two 6-sided die, what is the optimal strategy? Why is this the optimal strategy?

   2. If the host chooses a 3-sided die and a 12-sided die, what is the optimal strategy? Is there an optimal strategy? Why or why not?

   3. How is the optimal strategy affected by the number of faces on each die? What happens when each die has the same number of faces? What happens when each die has a different number of faces?

3. Keep track of the bingo calls and collect them in a sample.

   1. After a few rounds, create a dot plot of the bingo calls. Describe the distribution. What type of shape does it have? Where is it centered?

   2. Play a few more founds. Add the results to the dot plot. How has this altered the distribution from part a?

Teacher Notes

• For the first round, allow students to judge the constraints of the problems themselves. When rolling two 6-sided die, the only possible values are 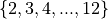. If students choose numbers outside of this range, have them draw the sample space the sample space with a tabl or tree diagram.

• Probability Bingo should be played initially with two 6-sided die. When each die has the same number of faces, the symmetry in the outcomes makes the optimal strategy easy to understand. After a few rounds, once the students start to understand the logic of the game, change it up by using different combinations of dice (i.e., a 3-sided die and a 12 sided die).