!: Factorials#

Introduction#

A factorial 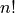$n!$ is a type of mathematical operation that needed in probability calculations (among other places). Factorials arise through application of the Fundamental Counting Principle (TODO: insert link), as we shall presently see.

The definition of a factorial is given by,

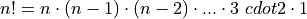
$n! = n \cdot (n -1) \cdot (n-2) \cdot ... \cdot 3 \ cdot 2 \cdot 1$

Note, this definition does not work when the value of n is 0. For this reason, we define,

$0! = 1$

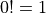
Calculator#

Problems#

Six friends Andy, Brandy, Candy, Dandy, Tandy, and Bob want to sit in a row at the cinema. If there are only six seats available, how many ways can we seat these friends?
Five names are written on slips of paper and placed into a hat. How many ways can these names be drawn without replacement from the hat?
Five names are written on slips of paper and placed into a hat. How many ways can three of these names be drawn without replacement from the hat?
How many 4 digit numbers can be formed from the digits 1, 3, 5, 7, and 8 if none of these appears more than once in each number?
You have invited 6 friends to a dinner party. How many different seating arrangements around the dining table are possible?
A class of six students has three boys and three girls. How many ways can the students stand in line so that boys and girls alternate?
A class of seven students has four boys and three girls. How many ways can the students stand in line so that boys and girls alternate?

Solutions#

TODO: jquery these into hidden elements

1: 720
2: 120
3: 20
4: 120
5: 5040
6: 72
7: 144