Ctrl+K

NPR: Permutations

NPR: Permutations#

A permutation is defined as the number of ways r objects can be selected from a total of n objects, where order is important. The number of permutations can be calculated with the following formula,

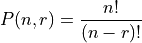
P(n,r) = \frac{n!}{(n-r)!}

This formula is easily derived with the Generalized Counting Principle. If you are doing these classwork, then we have probably already covered the permutation formula in class in detail. If not, head over to the Notes section and read through the part on Permutations (TODO: link).

The stipulation that order is important can be understood with a simple example. If we have two objects, say a and b, the sequences ab and ba are considered distinct permutations. In other words, 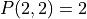P(2,2) = 2.

Calculator#

Warning

On the the TI-83s and the older model TI-84s, you must first type in n, the numbers of objects from which you are selecting, then insert a NPR function, and finally r, before executing the function. In other words, if you have 10 objects and you want to know the number of ways you can choose 2 of them where order matters, you would type into the main screen,

10 NPR 2

Problems#

  1. Five friends have gathered to take a group photo. The photographer wants them to form two rows. The first row will have three people, while the second row will have two people.

    1. How many possible arrangements can the photographer make for the first row?

    2. How many possible arrangements can the photographer make for the second row?

    3. If the photographer has already selected three friends for the first row, how many possible arrangements can she make for the second row?

    4. If the photographer has already selected two friends for the second row, how many possible arrangements can she make for the first row?

    5. What is the total amount of arrangements of friends that it is possible for the photographer to make?

    6. What is the connection between the answers to part a through e? Write a few sentences explaining the results.

  2. Ten students in the student body are eligible to run for student government. Six of them are male and four of them are female. There are three positions on the student government: president, secretary and treasurer.

    1. How many ways can the student government be formed of only males?

    2. How many ways can the student government be formed of only females?

    3. How many total ways can the student body be formed, regardless of gender?

    4. How many ways can the student government be formed so that at least one male and at least one female are included?

Solutions#

TODO: jquery these into hidden elements

  • 1a: 60

  • 1b: 20

  • 1c: 2

  • 1d: 6

  • 1e: 120

  • 2a: 120

  • 2b: 24

  • 2c: 720

  • 2d: 576

Contents