BINOMPDF: Binomial Probabilities

Introduction

A Binomial Random Variable counts the number of successes in ``n`` independent trials, where each trial has the same probability  of success and the same probability of failure. The precise conditions for a Binomial Random Variable are as follows,

Conditions for Binomial Random Variable

1. There are only two outcomes, a success or a failure, for each trial.

2. The same experiment is repeated a fixed number of times, ``n``.

3. The trials are independent; that is, the outcome of any particular trial does not affect the outcome of any other trial.

4. The probability of success remains the same for every trial.

The Binomial Probability Density Function is derived by application of the Fundamental Counting Principle and the multiplication laws of probability. For example, if we have 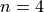trials and we are interested in the probability of getting 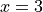successes, then we have to account for all the ways we can get 3 successes out of 4 trials. The sequences which correspond to this condition are given by,

sssf ssfs sfss fsss

Where s represents a success and f represents a failure. In other words, the total number of ways to get three successes from four trials is given by the number of combinations :math:C(4,3). Generalizing this idea, the number of ways to get ``x`` successes out of ``n`` trials is given by .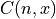

Since the trials are independent, the probability of any single sequence is given by the product of the probabilities of each individual trial. In the case of three successes out of four trials,

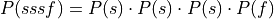
Generalizing this idea, the probability of a sequence of x successes and n-x failures is given by,

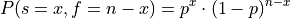
Keep in mind, this is the probability of one particular way of getting ``x`` successes from n trials. We have to account for all the different combinations that result in  successes. Therefore, the probability density of a Binomial Random Variable is given by,

Calculator

Binomial Probability Density Function

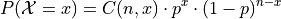
To calculate a Binomial probability on a TI-83/84 calculator, type in the following commands,

• 

• 

• 

The BINOMPDF function requires three arguments,

1. n: The number of independent trials.

2. p: The probability of success for a single trial.

3. x: The number of successes whose probability is sought.

Problems

1. Answer the following question without the BINOMPDF function. A fair coin is flipped ten times. Find the probability of getting exactly three heads.

   1. How many trials are being performed in this experiment?

   2. What is the probability of success for a single trial in this experiment?

   3. How many ways are there to get 3 heads from 10 coin flips?

   4. What is the probability of a single sequence of 3 heads and 7 tails?

   5. What is the probability of getting three heads if you flip a coin ten times?

2. If a basketball player makes 3 out of every 4 free throws, what is the probability that he will make 7 out of 10 free throws in a game? Round to three decimal spots.

3. If you roll a dice 9 times, what is the probability of getting exactly 2 faces that land on a 6? Round to three decimal places.

4. Uh oh! Sejal didn’t study and now there’s a pop quiz in AP Statistics that consists of 10 multiple choice questions. Each question has four possible answers, but only one is correct. In order to pass, a student must score a 7 or greater. If Sejal randomly guesses on each question, what is the probability she passes the pop quiz? Round to three decimal spots.

Solutions

TODO: jquery these into hidden elements

• 1a: 10

• 1b: 0.5

• 1c: 120

• 1d: 0.0009765625

• 1e: 0.1171875

• 2: 0.25

• 3: 0.279

• 4: 0.004