Ctrl+K

Simulations

Simulations#

The simulations in this section are meant to give students hands-on experience with randomness and uncertainty, and to get familiar with arguments involving probability. Each simulation and demonstration relies on an understanding of the Law of Large Numbers (todo: link). Before tackling any of these demos, it is recommended to discuss this concept in class beforehand.

Rice#

The experiment in this section provides an intuitive understanding of the Central Limit Theorem. Students will create a Normal distribution using grains of rice and then estimate its standard deviation using the Empirical Rule (TODO: link).

Select two volunteers. One student will hold a funnel above a large cafeteria tray. Another student will be given a large container of dry rice. The student with the container of rice will then begin to slowly pour the rice into the funnel.

It is important the student with the funnel hold it absolutely still. In addition, this experiment works best if the student dispensing the rice dispenses it extremely slowly in a circular motion around the rim, so as to give the rice enough time to clear the funnel. Otherwise, the rice is liable to become stuck in the funnel and lead to inaccurate results.

(TODO: diagram)

If everything goes according to plan, the rice should form a three dimensional Normal curve on the tray. As the Normal curve begins to accumulate, start a discussion about why the curve is Normal.

This can be explained as follows: The grains of rice satisfy the conditions of the Central Limit Theorem.

The Central Limit Theorem requires the observations in a sample to be drawn from the same population. This condition is met by forcing the grains of rice to go through the funnel and travel roughly the same trajectory (as determined gravity). The trajectory travelled by each grain represents the population distribution.

The Central Limit Theorem requires many observations. This condition is met by the numerous grains of rice. The grains represent a large sample.

The Central Limit Theorem also requires the independence of each observation. This is often the hardest condition for the students to understand in this context, since it would appear each grain of rice is affected by the actions of its falling neighbors.

The type of motion exhibited by the grains of rice is known as Brownian Motion (TODO: link). The best analogy to explain the independence of grains is a Plinko machine (TODO: link).

(TODO: plinko machine)

In Plinko, a ball is dropped and bounces off pegs at random as it descends towards the goal, sometimes falling to the right, sometimes falling to the left. The net effect of the bouncing, on average, cancels out and leads to the ball falling roughly where it was dropped. In other words, the best strategy in Plinko is to drop the ball right above the hole (assuming the peg sizes are uniform).

Once the curve is formed, take out the tape measure. Measure the width of the curve from one end to the other. You will likely have to ignore a few outlying grains of rice.

The Empirical Rule (todo: link) states 99.7% of a Normal distribution can be captured by moving a distance of 3 standard deviations, 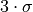3 \cdot \sigma, in either direction of the mean. In other words, the width you just measured should be roughly 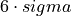6 \cdot sigma wide. This allows the population standard deviation to be calculated, i.e. by dividing the width of the curve by 6.

Approximate the center (mean) of the distribution by finding the midpoint of the curve width. Then mark off a distance of one standard deviation on either side of the center (mean). Separate the tails of the distribution from the middle of the distribution.

(TODO: diagram)

Collect the grains of rice in the tails in one of the volumetric flasks and collect the middle into the other volumetric flask. Level out the rice by shaking the flask and the measure the volume.

The ratio of the volume of the middle to the total volume should be roughly 68%, by the Empirical Rule.

Skittles#

TODO: explain

Foul Shot#

TODO: explain

Binomial#

Coin Flip#

TODO: explain

Die Roll#

TODO: explain

Geometric#

The experiments in this section are meant to demonstrate the distribution shape of a Geometric Random Variable. These demonstrations should be performed one after another. This will allow the students to see the differences in the two dot plots that are generated and internalize the meaning of the parameter p, the probability of success, for the Geometric Distribution.

Coin Flip#

In this demonstrations, students will be flipping a coin and counting the number of flips it takes until they get their first head. A success in this experiment corresponds to the outcome of the coin landing on heads.

Discussion Question

What is the probability of success in this Geometric experiment?

  1. Draw a dot plot on the board, as shown below. Note the horizontal axis should extend to 10 or more, to account for extreme outcomes.

(TODO: insert graph)

  1. Give each student a coin.

  2. Have each student flip the coin, counting the number of flips as they go. When it lands on heads the first time, the experiment is over.

  3. For each experiment they perform, have each student add a dot to the dot plot. The dot should be placed at the number corresponding to the total number of flips in the experiment.

  4. Repeat the process until the dot plot has 30 or more data points.

  5. Once the dot plot is constructed, have the students create a relative frequency distribution.

Discussion Question

How is the sample mean of the distribution related to the probability of success?

Die Roll#

In this demonstrations, students will be rolling a die and counting the number of rolls it takes until they get their first 5. A success in this experiment corresponds to the outcome of rolling a 5.

Discussion Question

What is the probability of success in this Geometric experiment?

  1. Draw a dot plots on the board, as shown below. Note the horizontal axis should extend to 20 or more, to account for extreme outcomes.

(TODO: insert graph)

  1. Give each student a six-sided die.

  2. Have each student flip the coin, counting the number of flips as they go. When it lands on heads the first time, the experiment is over.

  3. For each experiment they perform, have each student add a dot to the dot plot. The dot should be placed at the number corresponding to the total number of flips in the experiment.

  4. Repeat the process until the dot plot has 30 or more data points.

  5. After the dot plot is constructed, have the students create a relative frequency distribution.

Discussion Question

How is the sample mean of the distribution related to the probability of success?

Analysis#

Have the students answer the following questions.

  1. Compare and contrast the distribution of coin flips with the distribution of die rolls. How do measures of center compare? How do measures of variation of compare?

  2. Based on the answer to #1, what is the relationship between the probabiltiy of success, 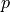p, and the standard deviation, 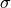\sigma, of the distribution?

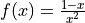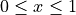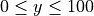  1. Using a graphing utility, plot the variance of a Geometric distribution as function of the probability of success, f(x)=\frac{1-x}{x^2}. Ensure the graping window is set to 0 \leq x \leq 1 and 0 \leq y \leq 100.

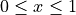    1. Why is it necessary to set the view window to 0 \leq x \leq 1?

    2. What happens to the variance as the probability of success approaches 1? Interpret this result in context.

    3. What happens to the variance as the probability of success approaches 0? Interpret this result in context.

Contents