Binomial Distribution

Contents

Binomial Distribution#

Binomial Random Variable#

Definition#

Recall a Bernoulli Random Variable is defined over a sample space of binary outcomes, a success s that occurs with probability 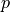$p$ of success and a failure f that occurs with probability 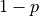$1-p$ ,

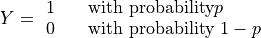
$Y = \begin{array}{ c l } 1 & \quad \textrm{with probability} p \\ 0 & \quad \textrm{with probability } 1 - p \end{array}$

Consider a random variable defined as the sum of 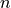$n$ Bernoulli random variables,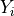 $Y_i$

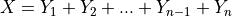
$X = Y_1 + Y_2 + ... + Y_{n-1} + Y_n$

Where each 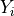$Y_i$ takes the value 1 with probability 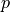$p$ or it takes the value 0 with probabilitiy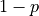 $1 - p$

TODO

From Conditional Probability, the probability of an intersection of independent events is the product of individual probabilitiy,

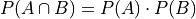
$P(A \cap B) = P(A) \cdot P(B)$

TODO

Conditions#

In order for an experiment to be Binomial, the experiment must the conditions just discussed. The summary below provides a list of each condition.

Parameters#

The Binomial Distribution has two parameters.

TODO

(Source code, png, hires.png, pdf)

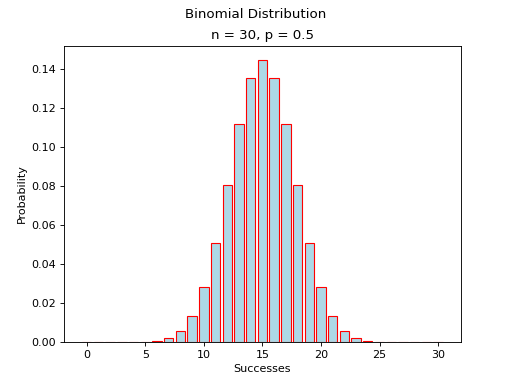
../../_images/binomial_distribution_01.png

(Source code, png, hires.png, pdf)

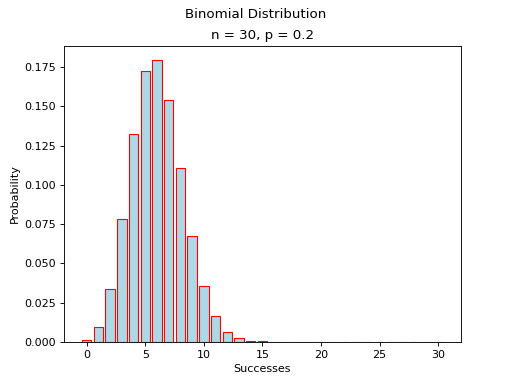
../../_images/binomial_distribution_02.png

(Source code, png, hires.png, pdf)

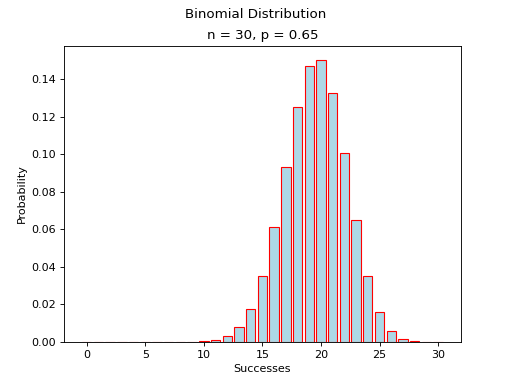
../../_images/binomial_distribution_03.png

(Source code, png, hires.png, pdf)

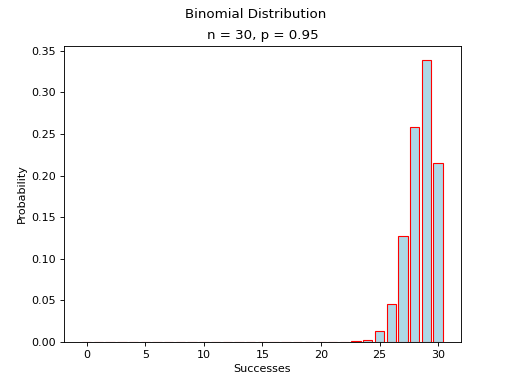
../../_images/binomial_distribution_04.png

Probabilitiy Distribution#

TODO

Probability Density Function#

TODO

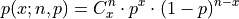
$p(x; n, p) = C^{n}_x \cdot p^{x} \cdot (1 - p)^{n-x}$

Cumulative Distribution Function#

TODO

By definition,

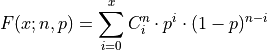
$F(x; n, p) = \sum^{x}_{i=0} C^{n}_i \cdot p^{i} \cdot (1 - p)^{n-i}$

Expectation#

TODO

derive through rules of independent random variable sums

TODO

Standard Deviation#

TODO

TODO

TODO

derive through rules of independent random variable sums