DRAW: Normal Approximation to Binomial#

Introduction#

When certain conditions are met, the Binomial Distribution can be approximated by the Normal Distribution. On this page, we will examine which conditions must be satisfied before the approximation can be applied successfully.

Activity#

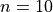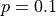First, let’s create a simple Binomial Distribution with $n = 10$ and $p = 0.1$ . In order to do this, we must first generate its domain, 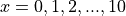$x=0, 1, 2, ..., 10$ , and store it in :math:L_1.

To do this, you can either go into the STAT editor and manually enter the list, element by element, or you can use the SEQ function to generate the list programmatically. Either way will work! The command below shows how to store the sequence in the 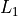$L_1$ ,

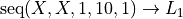
$\text{seq}(X, X, 1, 10, 1) \rightarrow L_1$

Then we calculate the value of the BINOMPDF at each value in the domain with the BINOMPDF function and store the result in 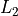$L_2$ . The command below shows how to store Binomial probabilities in $L_2$ ,

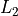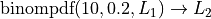
$\text{binompdf}(10,0.2, L_1) \rightarrow L_2$

Turn on your STATPLOT and create a histogram using 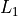$L_1$ as your XLIST and 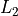$L_2$ as your FREQ.

Question #1

Describe the shape of the histogram. Explain why the Normal Distribution would not be a good approximation to Binomial Distribution with n = 10 and p = 0.1.

TODO: the rest .

DRAW: Normal Approximation to Binomial

Contents

DRAW: Normal Approximation to Binomial#

Introduction#

Activity#