Related Rates#
Water is draining out of the bottom of a 5000-gallon tank. The volume V of the water (in gallons) remaining in the tank after t minutes is given by the following formula:
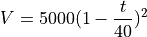
Find a formula for
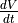 in terms of t.
in terms of t.How quickly is the water initially draining from the tank?
How quickly is the water draining from the tank at
 ?
?
In the theory of electrical circuits, Ohm’s Law describe the relationship between the voltage V across a resistor, the electrical current I passing through the resistor, and a quantity R known as the resistance. The law can be written as follows:
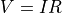
Usually voltage is measured in volts, current is measured in amperes (amps), and resistance is measured in ohms, where 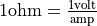 . In a circuit with variable resistance, the quantities V, I and R, all depend on time.
. In a circuit with variable resistance, the quantities V, I and R, all depend on time.
Take the derivative of Ohm’s Law to find an equation relating
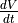 ,
, 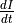 and
and 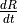 .
.Suppose the current is increasing at a rate of
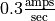 , while the resistance is holding steady at 4 ohms. How quickly is the voltage across the resistor increasing?
, while the resistance is holding steady at 4 ohms. How quickly is the voltage across the resistor increasing?Now suppose the voltage across the resistor is held constant at 20 volts, while the resistance is steadily increased at a rate of
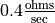 . What is the current through the resistor when the resistance reaches 10 ohms?
. What is the current through the resistor when the resistance reaches 10 ohms?In the same scenario as part c, at what rate is the current changing at that time? Is it increasing or decreasing?
Boat A is sailing north away from a dock, while boat B is sailing west towards the same dock:
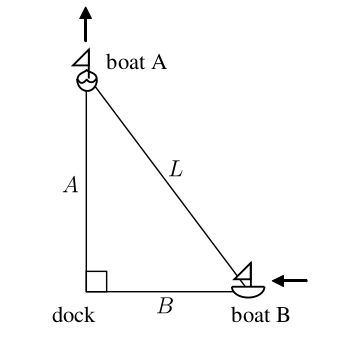
Find an equation that relates
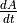 ,
, 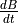 and
and 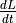 .
.Is
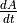 positive or negative? What about
positive or negative? What about 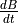 ? Explain.
? Explain.Suppose that boat A is 30 kilometers north of the dock, and is sailing north at a rate of
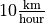 . Meanwhile, boat B is 40 kilometers east of the dock and is sailing west at a rate of
. Meanwhile, boat B is 40 kilometers east of the dock and is sailing west at a rate of 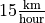 . What is the present distance between the two boats?
. What is the present distance between the two boats?In the same scenario as part c, what is
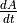 ?? What is
?? What is 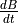 ?
?
In the same scenario as part c and part d, how quickly is the distance between the boats changing? Is the distance increasing or decreasing?
A positively charged particle is flying in the vicinity of a charged conductor. The electric potential energy of the particle is given by the formula,
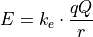
Where q is the charge of the particle, Q is the charge on the conductor and r is the distance between them. 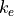 is an electrical field constant with a known value of
is an electrical field constant with a known value of 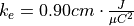 .
.
Assuming q and Q are constant, find a formula for
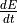 in terms of q, Q,
in terms of q, Q, 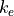 , r and
, r and 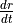 .
.At a certain instant, a particle with a charge of
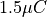 is 20 centimeters away from a conductor, and is flying directly towards the conductor at a rate of
is 20 centimeters away from a conductor, and is flying directly towards the conductor at a rate of 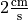 . Given that the conductor has a charge of
. Given that the conductor has a charge of 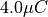 , how quickly is the electrical potential energy of the particle increasing?
, how quickly is the electrical potential energy of the particle increasing?
Boyle’s Law states that when a sample gas is compressed at a constant temperature, the pressure P and volume V satisfy the equation
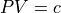 , where c is a constant. Suppose that at a certain instant, the volume is 600 cubic centimeters, the pressure is 150 kPA (kilo-pascals) and the pressure is increasing at a rate of
, where c is a constant. Suppose that at a certain instant, the volume is 600 cubic centimeters, the pressure is 150 kPA (kilo-pascals) and the pressure is increasing at a rate of 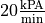 . At what rate is the volume decreasing at this instant?
. At what rate is the volume decreasing at this instant?