Sample Spaces#

Something

—Someone

TODO

Instructions#

1. Create a Python .py script named LASTNAME_FIRSTNAME_project_sEven.py in your Linux Files folder on your file system. You can do this by opening an IDLE session, creating a new file and then saving it. Replace LASTNAME and FIRSTNAME with your last and first name, respectively. 3. Create a docstring at the very top of the script file. Keep all written answers in this area of the script. 4. Read the project_seven_background section. 6. Perform all exercises and answer all questions in the Project section. Label your script with comments as indicated in the instructions of each problem. 7. When you are done, zip your script in a zip file named LASTNAME_FIRSTNAME_project_seven.zip 8. Upload the zip file to the Google Classroom Project Seven Assignment.

Background#

TODO

Cartesian Product#

Definition#

There are other types of Operations that we didn’t cover in class. One of the more important operations we skipped over is the Carteisan Product; we will now take the time to study this operation in particular, as it is helpful for understanding certain Sample Spaces and Events. Several of the problems in this lab will serve as illustrative examples so you may begin to understand what is meant by this operation.

We start with the formal definition. The Cartesian Product of two sets A and B, 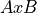$A x B$ , is defined as,

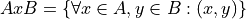
$A x B = \{ \forall x \in A, y \in B: (x, y) \}$

In plain English,

The Cartesian Product of two sets A and B, $A x B$ is the set of all ordered pairs (x, y) such that x belongs to A and y belongs to B.

An example will help to show what is meant. Consider the two sets A and B,

$A = \{ a, b, c \}$

$B = \{ d, e, f \}$

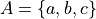
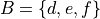
A simple way to visualize the Cartesian Product is by forming a table where the top row corresponds to the elements of A and the first column corresponds to elements of B. Then, in each entry, write the ordered pair formed by the intersection of rows and columns,

	a	b	c
d	(a,d)	(b,d)	(c,d)
e	(a,e)	(b,e)	(c,e)
f	(a,f)	(b,f)	(c,f)

The Cartesian Product is the set of all entries in this table,

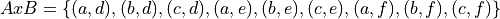
$A x B = \{ (a,d), (b,d), (c,d), (a,e), (b,e), (c,e), (a,f), (b,f), (c,f) \}$

Python#

You can generate a Cartesian Product in Python by using Comprehension.

One aspect of Comprehension we didn’t touch on when we first introduced it is the ability to chain together generator expressions to iterate over multiple lists simultaneously. Consider the following example,

pets = [ "dog", "cat", "fish" ]
owners = [ "cleopatra", "augustus", "napolean"]
pet_cross_owners = [ (o, p) for o in owners for p in pets]
print(pets_cross_owners)

Let’s break this example down.

The key point is: we are nesting a list iteration within another list iteration. When we write for p in pets, this tells Python to step through each element of the list pets, namely the elements dog, then cat, then fish. For each element of the pets list, we then tell Python to iterate over the next list with the expression for o in owners. This will iterate over the elements cleopatra, then augustus, then napolean, for each step in the first iteration. Then we glue the results together in an ordered pair (Tuples). This whole process is described below in sequence,

Iterate over pets
- Select element dog
  
  Iterate over owners
  
  Select element cleopatra
  
  Form ordered pair: (“dog”, “cleopatra”)
  
  Select element augustus
  
  Form ordered pair: (“dog”, “augustus”)
  
  Select element napolean
  
  Form ordered pair: (“dog”, “napolean”)
- Select element cat
  
  Iterate over owners
  
  Select element cleopatra
  
  Form orderer pair: (“cat”, “cleopatra”)
  
  Select element augustus
  
  Form ordered pair: (“cat”, “augustus”)
  
  Select element napolean
  
  Form ordered pair: (“cat”, “napolean”)
- Select element fish
  
  Iterate over owners
  
  Select element cleopatra
  
  Form ordered pair: (“fish”, “cleopatra”)
  
  Select element augustus
  
  Form ordered pair: (“fish”, “augustus”)
  
  Select element napolean
  
  Form ordered pair: (“fish”, “napolean”)

Note that in this example, since A is the set of pets and B is the set of owners, we can interpret 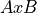$A x B$ as the set of all the possible Combinations of pet owners.

Project#

Using the cartesian_product, create a sample space that represents rolling two six-sided die.
- Print the results and include them in your report.
- Using the Length Function, find the total number of elements in the Cartesian Product.
- What is the probability of TODO (give ‘em a hard one)
Consider taking a two question multiple-choice pop quiz. Each question has four possible answers: a, b, c and d. Using the cartesian_product, create a sample space that represents all the different ways you can answer the questions on this pop-quiz.
- Print the results and include them in your report.
- What is the probability of getting a 100% of this quiz if you randomly guess an answer for each question?

Sample Spaces

Contents