Correlation#
If, in an expression (whose content need not be a judgeable content), a simple or complex symbol occurs in one or more places, and we think of it as replaceable at all or some of its occurrences by another symbol (but everywhere by the same symbol), then we call the part of the expression that on this occasion appears invariant the function, and the replaceable part its argument.
—Gottlob Frege, Begriffsschrift
Instructions#
Read the Background section.
Read the Correlation Function section. Follow along with the instructions in that section. Watch the accompanying video at the end of the section. Type each command as shown into your calculator to create the CORREL function.
Read the SSE Function section. Carefully read the SSE function requirements. Create the indicated function so that it fulfills the given requirements.
On the project due date, plug your calculator into the ViewSonic in the classroom and export your programs for grading. At the end of the project, you should have two functions CORREL and SSE. These functions must satisfy the requirements given in each of the sections below.
Background#
TODO
TI Basic#
TODO
Bivariate Statistics#
TODO
Correlation#
TODO
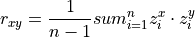
TODO
SSE#
TODO
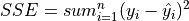
TODO
Correlation Function#
TODO
Video#
The following video walks you through creating the CORREL function on your calculator.

SSE Function#
TODO