Ctrl+K

Sampling Distributions

Sampling Distributions#

  1. 2014, Free Response, #3

Schools in a certain state receive funding based on the number of students who attend the school. To determine the number of students who attend a school, one school day is selected at random and the number of students in attendance that day is counted and used for funding purposes. The daily number of absences at High School A in the state is approximately normally distributed with mean of 120 students and Standard deviation of 10.5 students.

  1. If more than 140 students are absent on the day the attendance count is taken for funding purposes, the school will lose some of its state funding in the subsequent year. Approximately what is the probability that High School A will lose some state funding?

  2. The principals’ association in the state suggests that instead of choosing one day at random, the state should choose 3 days at random. With the suggested plan, High School A would lose some of its state funding in the subsequent year if the mean number of students absent for the 3 days is greater than 140. Would High School A be more likely, less likely, or equally likely to lose funding using the suggested plan compared to the plan described in part a? Justify your choice.

  3. A typical school week consists of the days Monday, Tuesday, Wednesday, Thursday, and Friday. The principal at High School A believes that the number of absences tends to be greater on Mondays and Fridays, and there is concern that the school will lose state funding if the attendance count occurs on a Monday or Friday. If one school day is chosen at random from each of 3 typical school weeks, what is the probability that none of the 3 days chosen is a Tuesday, Wednesday, or Thursday?

  1. 2006, Free Response, #3

The depth from the surface of Earth to a refracting layer beneath the surface can be estimated using methods developed by seismologists. One method is based on the time required for vibrations to travel from a distant explosion to a receiving point. The depth measurement M is the sum of the true depth D and the random measurement error E. That is, 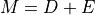M = D + E. The measurement error E is assumed to be normally distributed with mean 0 feet and standard deviation 1.5 feet.

  1. If the true depth at a certain point is 2 feet, what is the probability that the depth measurement will be negative?

  2. Suppose three independent depth measurements are taken at the point where the true depth is 2 feet. What is the probability that at least one of these measurements will be negative?

Hint

What is the complement of “at least one”? Refer to Aristotle’s Square of Opposition!

  1. What is the probability that the mean of the three independent depth measurements taken at the point where the true depth is 2 feet will be negative?

  1. 2004, Free Response Form B, #3

Trains carry bauxite ore from a mine in Canada to an aluminum processing plant in northern New York state in hopper cars. Filling equipment is used to load ore into the hopper cars. When functioning properly, the actual weights of ore loaded into each car by the filling equipment at the mine are approximately normally distributed with a mean of 70 tons and a standard deviation of 0.9 ton. If the mean is greater than 70 tons, the loading mechanism is overfilling.

  1. If the filling equipment is functioning properly, what is the probability that the weight of the ore in a randomly selected car will be 70.7 tons or more? Show your work.

  2. Suppose that the weight of ore in a randomly selected car is 70.7 tons. Would that fact make you suspect that the loading mechanism is overfilling the cars? Justify your answer.

  3. If the filling equipment is functioning properly, what is the probability that a random sample of 10 cars will have a mean ore weight of 70.7 tons or more? Show your work.

  4. Based on your answer in part (c), if a random sample of 10 cars had a mean ore weight of 70.7 tons, would you suspect that the loading mechanism was overfilling the cars? Justify your answer.

  1. 2007, Free Response, #3

Big Town Fisheries recently stocked a new lake in a city park with 2,000 fish of various sizes. The distribution of the lengths of these fish is approximately normal.

  1. Big Town Fisheries claims that the mean length of the fish is 8 inches. If the claim is true, which of the following would be more likely?

    A random sample of 15 fish having a mean length that is greater than 10 inches

or

A random sample of 50 fish having a mean length that is greater than 10 inches

Justify your answer.

  1. Suppose the standard deviation of the sampling distribution of the sample mean for random samples of size 50 is 0.3 inch. If the mean length of the fish is 8 inches, use the normal distribution to compute the probability that a random sample of 50 fish will have a mean length less than 7.5 inches.

  2. Suppose the distribution of fish lengths in this lake was nonnormal but had the same mean and standard deviation. Would it still be appropriate to use the normal distribution to compute the probability in part b ? Justify your answer.

  1. 2008, Free Response Form B, #2

Four different statistics have been proposed as estimators of a population parameter. To investigate the behavior of these estimators, 500 random samples are selected from a known population and each statistic is calculated for each sample. The true value of the population parameter is 75. The graphs below show the distribution of values for each statistic.

../../../_images/2006_apstats_frp_formb_04.png

  1. Which of the statistics appear to be unbiased estimators of the population parameter? How can you tell?

  2. Which of statistics A or B would be a better estimator of the population parameter? Explain your choice.

  3. Which of statistics C or D would be a better estimator of the population parameter? Explain your choice.

  1. 2009, Free Response, #2

A tire manufacturer designed a new tread pattern for its all-weather tires. Repeated tests were conducted on cars of approximately the same weight traveling at 60 miles per hour. The tests showed that the new tread pattern enables the cars to stop completely in an average distance of 125 feet with a standard deviation of 6.5 feet and that the stopping distances are approximately normally distributed.

  1. What is the 70th percentile of the distribution of stopping distances?

  2. What is the probability that at least 2 cars out of 5 randomly selected cars in the study will stop in a distance that is greater than the distance calculated in part a?

  3. What is the probability that a randomly selected sample of 5 cars in the study will have a mean stopping distance of at least 130 feet?

  1. 2010, Free Response, #2

A local radio station plays 40 rock-and-roll songs during each 4-hour show. The program director at the station needs to know the total amount of airtime for the 40 songs so that time can also be programmed during the show for news and advertisements. The distribution of the lengths of rock-and-roll songs, in minutes, is roughly symmetric with a mean length of 3.9 minutes and a standard deviation of 1.1 minutes.

  1. Describe the sampling distribution of the sample mean song lengths for random samples of 40 rock-and-roll songs.

  2. If the program manager schedules 80 minutes of news and advertisements for the 4-hour (240-minute) show, only 160 minutes are available for music. Approximately what is the probability that the total amount of time needed to play 40 randomly selected rock-and-roll songs exceeds the available airtime?

  1. 2019, Free Response, #6

TODO (THIS IS A GOOD ONE TO GO OVER IN GREAT DETAIL!)