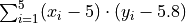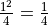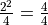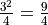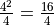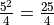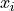Ctrl+K

Sums

Sums#

Warning

There will be many obligatory sum puns on this page.

Something About Sums#

Some mathematical expressions are sums.

Warning

Told you.

A sum is a type of operation, like +, -, x and % (addition, subtraction, multiplication, division), but there is a key difference. The arithmetic operations mentioned in the previous sentence operate on numbers. The sum symbol operates on sets.

Some Anatomy of Sums#

Note

\sum is the capital Greek letter, epsilon.

The different parts of the sum are: the upper limit, the lower limit, the term and the index. These components can be identified with the following diagram,

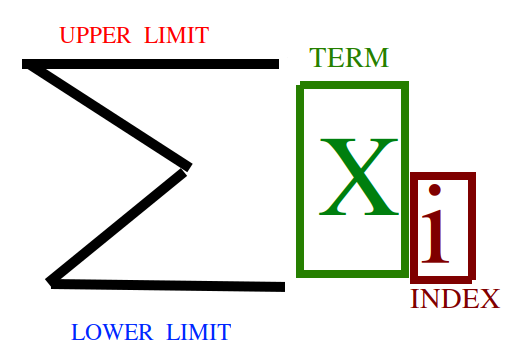
../../../_images/summation_symbol.png

A sum contains two important bits of information:

  1. Instructions on how to construct each term.

  2. Instructions on how to combine each term.

Some Examples of Sums#

Example 1#

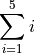
\sum_{i=1}^{5} i

Let’s break it down, term by term. The first set of instructions a sum gives us is instructions on how to construct each term of the sum. The index tells us to look at the numbers 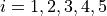i = 1, 2, 3, 4, 5 and then create the term 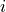i for each one. We start at 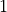1 because the lower limit is 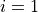i = 1. We go up to 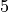5 because the upper limit is 5.

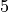Important

The index of a sum always increases by one, as you move from term to term.

A table will help visualize this,

Index

1

2

3

4

5

Term

1

2

3

4

5

In this case, each term is equal to the index because the expression that defines the term is just 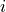i.

Now that we know what each term of the sum is, we move on to the instructions that tell us how to combine these terms. To sum, we take each term of the set (the bottom row of the table) and add it up,

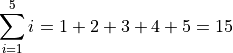
\sum_{i=1}^5 i = 1 + 2 + 3 + 4 + 5 = 15

Example 2#

Let’s make it more complicated. Suppose you were given the expression,

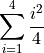
\sum_{i=1}^{4} \frac{i^2}{4}

In the same fashion, we first determine the terms of the sum by looking at the values of the index for 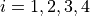i=1,2,3,4 (from the lower limit to the upper limit)

Index

1

2

3

4

5

Term

\frac{1^2}{4} = \frac{1}{4}

\frac{2^2}{4} = \frac{4}{4}

\frac{3^2}{4} = \frac{9}{4}

\frac{4^2}{4} = \frac{16}{4}

\frac{5^2}{4} = \frac{25}{4}

Then, once we have each one, we add up each term,

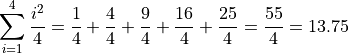
\sum_{i=1}^{4} \frac{i^2}{4} = \frac{1}{4} + \frac{4}{4} + \frac{9}{4} + \frac{16}{4} + \frac{25}{4} = \frac{55}{4} = 13.75

Sum Complications#

Sometimes sums do not tell us how to make the terms of the summation; sometimes they tell us what the terms are. In other words, rather than giving us a formula involving the index, sometimes a sum will tell you to take terms from a particular sample (also known mathematically as a set).

Example 3#

Suppose you were given the following sample (set),

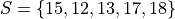
S = \{ 15, 12, 13, 17, 18 \}

Each individual in this sample (set) can be indexed,

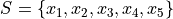
S = \{ x_1, x_2, x_3, x_4, x_5 \}

Where we have indexed each observation according to the scheme,

i

x_i

1

15

2

12

3

13

4

17

5

18

If you are given a sample (set) and you encounter a sum that looks like,

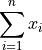
\sum_{i=1}^n x_i

This type of sum is telling you to take each term (member) of the indexed sample (set) and sum them up.

Going back to the example,

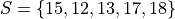
S = \{ 15, 12, 13, 17, 18 \}

We can calculate the sum of this sample (set) 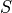S by summing up each term,

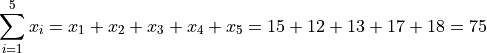
\sum_{i = 1}^5 x_i = x_1 + x_2 + x_3 + x_4 + x_5 = 15 + 12 + 13 + 17 + 18 = 75

Problems#

  1. Given

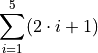
\sum_{i=1}^5 (2\cdot i + 1)

  1. Find the terms of the summation by filling out the table,

    Index

    1

    2

    3

    4

    5

    Term

    ?

    ?

    ?

    ?

    ?

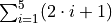
  2. Calculate the sum \sum_{i=1}^5 (2\cdot i + 1)

  1. Given

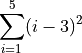
\sum_{i=1}^5 (i - 3)^2

  1. Find the terms of the summation by filling out the table,

    Index

    1

    2

    3

    4

    5

    Term

    ?

    ?

    ?

    ?

    ?

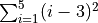
  2. Calculate the sum \sum_{i=1}^5 (i - 3)^2

  1. Given

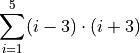
\sum_{i=1}^5 (i-3) \cdot (i + 3)

  1. Find the terms of the summation by filling out the table,

    Index

    1

    2

    3

    4

    5

    Term

    ?

    ?

    ?

    ?

    ?

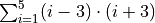
  2. Calculate the sum \sum_{i=1}^5 (i-3) \cdot (i + 3)

  1. Given

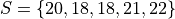
S = \{ 20, 18, 18, 21, 22 \}

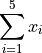
\sum_{i=1}^{5} x_i

  1. Find the terms of the sumation by filling out the table,

    Index

    1

    2

    3

    4

    5

    Term

    ?

    ?

    ?

    ?

    ?

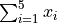
  2. Calculate the sum \sum_{i=1}^{5} x_i

  1. Given

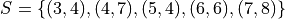
S = \{ (3,4), (4,7), (5, 4), (6, 6), (7, 8) \}

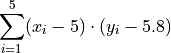
\sum_{i=1}^{5} (x_i - 5) \cdot (y_i - 5.8)

  1. Find the terms of the sumation by filling out the table,

    Index

    1

    2

    3

    4

    5

    Term

    ?

    ?

    ?

    ?

    ?

  2. Calculate the sum \sum_{i=1}^{5} (x_i - 5) \cdot (y_i - 5.8)

Contents