Ctrl+K

Geometric Distribution

Geometric Distribution#

  1. Conditions for Geometric Random Variable

Determine whether each of the following experiments satisfy the conditions for a Geometric Random Variable.

  1. TODO

  2. TODO

  3. TODO

  1. Probability Density

Use the Geometric Probability Density Function,

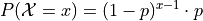
P(\mathcal{X}=x) = (1-p)^{x-1} \cdot p

to answer the following questions.

  1. If p=0.1, what is P(\mathcal{X}=1)?

  2. If p=0.1, what is P(\mathcal{X}=10)?

  3. If p=0.9, what is P(\mathcal{X}=1)?

  4. If p=0.9, what is P(\mathcal{X}=10)?

  5. Write a few sentences in plain English that explains how changing the parameter p of the Geometric Distribution affects the probability of its outcomes.

  1. Applications

Use the properties of probability and the Geometric Distribution to solve the following problems.

  1. From an ordinary deck of 52 cards, you draw cards at random and with replacement, until the first ace is drawn. what is the probability that atleast five draws are needed?

  2. A certain basketball player makes a foul shot 45% of the time. Suppose this player stands on the foul line and continues shooting until he makes two baskets. What is the probability that (i) the first basket occurs on the sixth shot? (ii) the first and second baskets occur on the fourth and eighth shots, respectively?

  3. The probability is 0.8 that Marty hits target M when he fires at it. The probability is 0.45 that Alvie hits target A when he fires at it. Marty and Alvie fire one shot each at their targets. If both of them hit their targets, they stop; otherwise, they will continue.

  1. What is the probability that they stop after 3 tries?

  2. What is the expected number of times they fire before stopping?

A.P. Exam Practice#

  1. 2016, Free Response, #4

A company manufactures model rockets that require igniters to launch. Once an igniter is used to launch a rocket, the igniter cannot be reused. Sometimes an igniter fails to operate correctly, and the rocket does not launch. The company estimates that the overall failure rate, defined as the percent of all igniters that fail to operate correctly, is 15 percent.

A company engineer develops a new igniter, called the super igniter, with the intent of lowering the failure rate.

To test the performance of the super igniters, the engineer uses the following process.

Step 1: One super igniter is selected at random and used in a rocket.

Step 2: If the rocket launches, another super igniter is selected at random and used in a rocket.

Step 2 is repeated until the process stops. The process stops when a super igniter fails to operate correctly or 32 super igniters have successfully launched rockets, whichever comes first. Assume that super igniter failures are independent.

  1. If the failure rate of the super igniters is 15 percent, what is the probability that the first 30 super igniters selected using the testing process successfully launch rockets?

  2. Given that the first 30 super igniters successfully launch rockets, what is the probability that the first failure occurs on the thirty-first or the thirty-second super igniter tested if the failure rate of the super igniters is 15 percent?

  3. Given that the first 30 super igniters successfully launch rockets, is it reasonable to believe that the failure rate of the super igniters is less than 15 percent? Explain.

  1. 2011, Free Response, #3

Warning

The problem requires more than the Geometric Distribution to solve.

An airline claims that there is a 0.10 probability that a coach-class ticket holder who flies frequently will be upgraded to first class on any flight. This outcome is independent from flight to flight. Sam is a frequent flier who always purchases coach-class tickets.

  1. What is the probability that Sam’s first upgrade will occur after the third flight?

  2. What is the probability that Sam will be upgraded exactly 2 times in his next 20 flights?

  3. Sam will take 104 flights next year. Would you be surprised if Sam receives more than 20 upgrades to first class during the year? Justify your answer.

Contents