Linear Regression#

TODO

Regression Model#

TODO

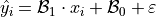
$\hat{y_i} = \mathcal{B}_1 \cdot x_i + \mathcal{B}_0 + \varepsilon$

Where the term $\varepsilon$ is a normally distributed error term centered around 0 with standard deviation equal to the mean squared error of the model,

$\varepsilon \sim \mathcal{N}(0, \text{MSE})$

TODO

Mean Squared Error#

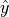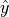The term $\hat{y}$ is not the observed value of $y$ in the bivariate sample of data that was used to calibrate the model. It is the predicted value of $y$ given the observed value of $x$ . This is an extremely important point when talking about regression. The model equation is a prediction, and the prediction is not exact. Each predicted value of $y$ , $\hat{y}$ , will deviate from the observed value of $y$ . The deviation, if the model is a good fit, should be normally distributed around 0.

TODO

SSE: Sum Squared Error#

TODO

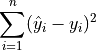
$\sum_{i=1}^{n} (\hat{y}_i - y_i)^2$

TODO

MSE: Mean Squared Error#

TODO

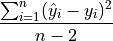
$\frac{\sum_{i=1}^n (\hat{y}_i - y_i)^2}{n-2}$

TODO

Model Coefficients#

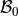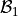The regression model coefficients can be estimated by finding the values of $\mathcal{B}_0$ and $\mathcal{B}_1$ that minimize the MSE of the model.

In other words,

TODO: example. plug in various values of coefficients and demonstrate the MSE varies. Show there is a value that produces a minimum.

Note

In order to derive an algebraic expression for the coefficients, differential calculus is required. If you want an extra credit assignment related to this, talk to me outside of class.

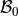
$\mathcal{B}_0$

TODO

$\mathcal{B}_1$

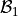
TODO

Line of Best Fit#

TODO

Linear Regression

Contents

Linear Regression#

Regression Model#

Mean Squared Error#

SSE: Sum Squared Error#

MSE: Mean Squared Error#

Model Coefficients#

Line of Best Fit#